Latihan Soal dan Jawaban Materi Matematika SMA: Eksponen

Dalam artikel ini, kamu akan menjumpai berbagai jenis latihan soal dan jawaban dari salah satu materi yang akan kamu jumpai di pelajaran matematika kelas 1 SMA, yaitu eksponen.

Penggunaan eksponen dalam kehidupan sehari-hari mungkin nggak begitu terlihat di sekitar kamu. Tetapi, angka kecil-kecil yang ada di atas sebuah bilangan ini membantu banget lho, buat para ilmuwan dan peneliti!

Lho, kok bisa gitu?

Ya bisa, dong! Tanpa kamu sadari, eksponen memegang peranan penting untuk profesi yang membutuhkan perhitungan dalam jumlah angka yang besar, seperti dalam bidang biologi (menghitung pertumbuhan bakteri), ekonomi (menghitung bunga majemuk), dan sosial (menghitung pertumbuhan penduduk).

Nggak perlu berlama-lama, yuk kita simak artikelnya dan kerjakan soal-soal yang tersedia agar pemahaman kamu semakin jelas.

1. Apa Sih, Eksponen Itu?
2. Eksponen Punya Sifat-Sifat?
3. Beri Aku Contoh Soalnya, Dong!

Apa Sih, Eksponen Itu?

Siapa nih yang masih ingat materi saat SMP dulu? Soalnya, materi tentang eksponen ini sudah pernah disinggung saat belajar matematika kelas 9, lho…

Jadi, eksponen adalah bentuk perkalian dengan bilangan yang sama secara berulang. Sederhananya, eksponen itu perkalian bertingkat pakai angka yang sama, gituuu. Eksponen punya nama lain, lho, yaitu bilangan berpangkat!

Meskipun judulnya perkalian, tapi kamu nggak hanya harus hapal perkalian, ya. Ada beberapa sifat eksponen yang juga harus kamu ketahui agar pemahaman kamu makin mantap.

Eksponen Punya Sifat-Sifat?

Punya, dong! Dengan sifat-sifat eksponen, kamu nggak perlu ribet mengalikan banyak angka hanya untuk mencari hasil dari satu bilangan eksponen. Sekarang, simak baik-baik ya!

Pangkat Penjumlahan

a (m) . a(n) = a (m + n) (perkalian eksponen dengan basis yang sama, maka pangkatnya harus ditambah)
Contoh: 4(2) . 4(3) = 4(2 + 3) = 4(5)

Pangkat Pengurangan

a (m):a (n) = a(m – n) (pembagian eksponen dengan basis yang sama, maka pangkatnya harus dikurang)
Contoh: 4(5) : 4(3) = 4(5 – 3) = 4(2)

Pangkat Perkalian

(a(m))(n) = a(m x n)(jika bilangan berpangkat dipangkatkan lagi, maka pangkatnya harus dikali)
Contoh: (4(2))(3) = 4(2 x 3) = 4(6)

Perkalian Bilangan yang Dipangkatkan

(a . b)(m) = a(m) . b(m) (perkalian bilangan yang dipangkatkan, maka masing-masing bilangan tersebut dipangkatkan juga)
Contoh: (3. 5)(2) = 3(2). 5(2)

Perpangkatan pada Bilangan Pecahan

Untuk bilangan pecahan yang dipangkatkan, maka bilangan pembilang dan penyebutnya harus dipangkatkan semua, dengan syarat nilai “b” atau penyebutnya tidak boleh sama dengan 0.

Pangkat Negatif

Pada sifat ini, jika (a(n))di bawah itu positif, maka saat dipindahkan ke atas menjadi negatif. Begitu juga sebaliknya, jika (a(n)) di bawah itu negatif, maka saat dipindahkan ke atas menjadi positif. Kita lihat rumus dan contohnya ya.

Pangkat Pecahan

Pada sifat ini, kamu bisa lihat, terdapat akar n dari a(m). Nah, ketika diubah jadi eksponen, akar n menjadi penyebut dan pangkat m menjadi pembilang, dengan syarat nilai n harus lebih besar atau sama dengan dua (n ≥ 2). Kita lihat rumus dan contohnya ya.

Pangkat Nol

a(0) = 1. Untuk sifat yang satu ini, syaratnya nilai a tidak boleh sama dengan 0 ya, karena kalo a = 0, maka hasilnya tidak terdefinisi.

Belajar Dari Contoh Soal, Yuk!

Contoh Soal 1: Sederhanakan Bentuk Eksponen

Soal:

Penyelesaian:
Gunakan sifat eksponen:

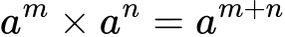
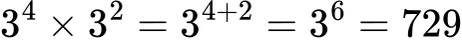
Jawaban:
729

Contoh Soal 2: Pembagian Eksponen

Soal:

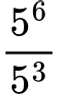
Penyelesaian:

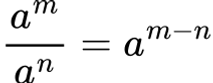
Gunakan sifat eksponen, maka:

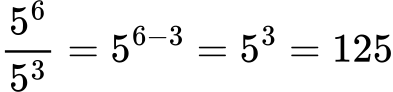
Jawaban:
125

Contoh Soal 3: Pangkat dalam Pangkat

Soal:

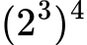
Penyelesaian:
Gunakan sifat eksponen:
Jika

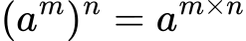
Maka:

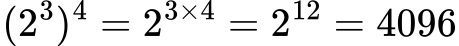
Jawaban:
4096