Artikel ini akan membahas mengenai serba-serbi bilangan rasional dan irasional, mulai dari pengertian, contoh, hingga contoh soalnya.
Sewaktu belajar matematika di sekolah dasar dulu, mungkin kamu sudah mengetahui kalau bilangan dalam matematika tidak hanya terdiri dari satu jenis. Hayo, ingat tidak? Ada yang namanya bilangan bulat, pecahan, desimal, dan lain sebagainya.
Nah, ketika kamu menjejaki tahap selanjutnya di bangku SMP, kamu akan mempelajari dua jenis bilangan baru, yakni bilangan rasional dan irasional. Secara keseluruhan, perbedaan utama yang bisa kamu jadikan acuan dalam membedakan antara bilangan rasional dan irasional terletak pada kemampuan masaing-masing jenis bilangan untuk ditulis dalam bentuk pecahan.
Bilangan rasional sendiri dapat dikatakan sebagai perbandingan dua bilangan bulat, sedangkan bilangan irasional tidak bisa. Rasional memiliki desimal yang berhenti atau berulang, sedangkan irasional memiliki desimal yang tidak berhenti dan tidak berulang. Keduanya sama-sama termasuk bilangan real, tetapi memiliki sifat yang sangat berbeda. Memahami perbedaan ini sangat penting dalam banyak bidang matematika, terutama dalam pemahaman konsep bilangan, pecahan, dan kalkulus.
Kedua jenis bilangan ini sama pentingnya dalam mengerjakan suatu proses serta masakah matematika. Seberapa penting sih, kedua jenis bilangan ini? Yuk, cari tahu bersama!
- Serba-Serbi Bilangan Rasional
- Serba-Serbi Bilangan Irasional
- Coba Lihat Contoh Soalnya, Yuk!
Serba-Serbi Bilangan Rasional
Bilangan rasional adalah bilangan yang dapat dinyatakan sebagai pecahan dari dua bilangan bulat, dengan penyebut (penyebut ≠ 0).
Bilangan rasional adalah bilangan yang dapat dituliskan sebagai pecahan dari dua bilangan bulat, seperti misalnya
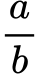
Dalam pecahan tersebut, a dan b merupakan bilangan bulat, dengan b≠0. Yuk, kita bahas lebih lanjut!
Dalam matematika, kata “rasional” berasal dari kata “rasio”, yang menandakan bahwa bilangan ini bisa dituliskan sebagai perbandingan dua bilangan. Misalnya, bilangan 3 adalah bilangan bulat, tetapi juga bilangan rasional karena dapat ditulis sebagai 3/1. Hal yang sama dapat diaplikasikan pada bilangan desimal seperti 0,75 adalah bilangan rasional karena 0,75 = 75/100 = 3/4.
Nah, prinsip yang sama juga termasuk ke dalam bilangan bulat (positif, negatif, nol), lho! Mulai dari semua pecahan biasa, dan semua desimal yang berakhir (seperti 0,5 atau 1,2) maupun desimal yang berulang (seperti 0,333… atau 1,272727…). Nilai di bawah ini juga merupakan bagian dari bilangan rasional, lho!
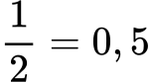
Hal yang penting untuk kamu catat adalah bilangan rasional selalu dapat diubah menjadi pecahan dengan pembilang dan penyebut bulat. Soalnya, bentuk ini bisa dibalik ke pecahan, dan kembali ke pengertian bilangan rasionnal itu sendiri yang bisa dinyatakkan dengan pecahan. Misalnya, 2,5 adalah desimal, tetapi juga rasional karena 2,5 = 5/2. Bilangan rasional juga termasuk dalam himpunan bilangan real, artinya bilangan rasional dapat digambarkan pada garis bilangan. Makanya, meskipun ada banyak bentuk bilangan rasional, semuanya bisa dihitung secara sistematis atau disebut “terhitung (countable)” dalam matematika.
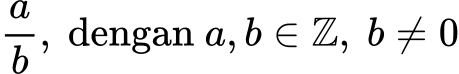
Di mana:
- a adalah pembilang (bilangan bulat)
- b adalah penyebut (bilangan bulat bukan nol)
Ciri-ciri Bilangan Rasional
Sekarang, kamu bisa mulai mempelajari soal ciri bilangan rasional dengan melihat beberapa ciri beriku, antara lain;
- Bisa ditulis sebagai pecahan biasa (misal: 2/3 atau-5/4)
- Bentuk desimalnya berhenti (terminating) atau berulang (repeating).
Maksudnya, bilangan desimal disebut terhenti (terminating) ketika angka yang terletak di belakang koma berhenti di satu posisi karena habis. Misalnya, 0,5. Sementara itu, bilangan desimal yang berulang (repeating) maksudnya adalah bilangan yang pentung desimalnya tidak berhenti, tapi berlanjut dan mengulangi pola yang sama secara terus menerus. Misalnya,
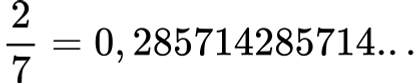
Contoh Bilangan Rasional
Gimana, guys? Dari penjelasan di atas, sudah ada gambaran kira-kira contoh bilangan yang termasuk ke dalam bilangan rasional itu, apa saja ya? Yuk, kita lihat contohnya di bawah!
- ½ (karena = 0,5)
- 4 (karena = 4/1)
- -0,25 (karena = -25/100)
- 0.333… (karena = 1/3, desimal berulang)
Serba-Serbi Bilangan Irasional
Berbanding terbalik dengan bilangan rasional yang sudah kita bahas di atas, bilangan irasional merupakan jenis bilangan yang tidak bisa dinyatakan dalam bentuk pecahan.
Jika kamu ingin mencoba membuktikan apakan sebuah bilangan dapat digolongkan ke dalam bilagan rasional atau irasional, kamu dapat mencoba mengubah bilangan tersebut dalam bentuk pecahan atau desimal. Jika bilangan tersebut tidak bisa dibuat ke dalam bentuk pecahan, serta memiliki bentuk desimal yang tak berhenti dan tidak berulang, kemungkinan besar bilangan tersebut adalah bagian dari bilangan irasional, guys!
Bilangan irasional memiliki desimal tak berakhir dan tak berulang, yang beraarti jenis bilangan yang satu ini tidak memiliki pola tertentu dan tidak berhenti. Apakah kamu familiar dengan bilangan ini?
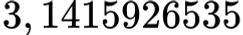
Bener banget, guys! Bilangan desimal di atas merupakan bentuk dari π (pi), salah satu bagian dari bilangan irasional paling terkenal di dunia. Ada juga bilangan lainnya, yaitu 2 (akar dua) yang nilainya sekitar 1,4142135…
Kalau kamu perhatikan, kedua bilangan tersebut tidak memiliki pola desimal yang berulang. Meskipun bisa didekati secara desimal, nilainya tidak bisa ditulis persis sebagai pecahan dengan bilangan bulat.
FYI untuk kamu nih, guys. Bilangan irasional biasanya muncul dari hasil akar bilangan yang bukan kuadrat sempurna (seperti √2, √3, √5, dll), atau dari konstanta matematika seperti π dan e.
Namun, kamu juga perlu ingat bahwa tidak semua akar adalah irasional. Jika akarnya menghasilkan bilangan bulat (seperti √9 = 3), maka bilangan tersebut tetap disebut dnegan bilangan rasional. Hal yang membuat bilangan irasional istimewa adalah karena mereka tidak bisa ditulis dalam bentuk yang pasti dan tidak bisa ditulis sebagai perbandingan dua bilangan bulat. Bahkan jika kita menggunakan kalkulator, hasilnya tetap hanya perkiraan.
Dalam matematika, bilangan irasional adalah bagian dari himpunan bilangan real, sama seperti bilangan rasional. Namun berbeda dengan bilangan rasional yang terhitung (countable), bilangan irasional bersifat tak terhitung (uncountable). Maksudnya, jumlahnya tidak dapat diurutkan atau dihitung satu per satu secara sistematis. Inilah yang membuat bilangan irasional menjadi bagian penting dalam teori bilangan dan kalkulus.
Ciri-ciri Bilangan Irasional
Sama seperti bilangan rasional, bilangan irasional juga memiliki beberapa ciri yang bisa kamu identifikasi, guys. Antara lain;
- Tidak dapat dinyatakan sebagai pecahan a/b
- Desimalnya tak berakhir (non-terminating) dan tidak berulang (non-repeating)
- Biasanya berasal dari akar bilangan yang tidak menghasilkan bilangan rasional atau konstanta khusus seperti π dan e
Contoh Bilangan Irasional
Seperti jenis bilangan sebelumnya, sekarang saatnya kamu mencari contoh bilangan irasional yang sering kamu jumpai dalam soal matematika.
- √2 (≈ 1.414213…, tak berhenti & tak berulang)
- π (pi ≈ 3.14159…, tak berakhir & tak berulang)
- e (bilangan Euler ≈ 2.71828…)
- √3, √5, dan akar bilangan prima lainnya
Coba Lihat Contoh Soalnya, Yuk!
Gimana ya, cara menyelesaikan contoh soal di bawah ini?
Tentukan apakah bilangan di bawah ini termasuk bilangan rasional atau irasional! Ubah ke bentuk desimalnya.
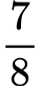
Melihat bilangan pecahan di atas, kira-kira bagaimana ya cara menyelesaikannya?
Kalau kamu perhatikan, bilangan di atas sudah ditulis dalam bentuk pecahan, di mana penjelasan mengenai bilangan rasional menyinggung hal ini. Ingatkah kamu apa maksudnya bilangan rasional?
Betul banget, guys! Bilangan rasional merupakan jenis bilangan yang dapat digambarkan dalam bentuk pecahan. Karenanya, bilangan di atas termasuk ke dalam bilangan rasional. Namun, karena soal tersebut menyebutkan bahwa pecahan tersebut harus dibuat ke dalam bentuk desimal, yuk selesaikan bersama!
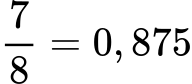
Bilangan desimal yang menjadi hasil akhir dari pecahan di atas merupakan jenis bilangan desimal terhenti (terminating). Hal ini menjadi bukti lain bahwa 7/8 merupakan bagian dari bilangan rasional.





